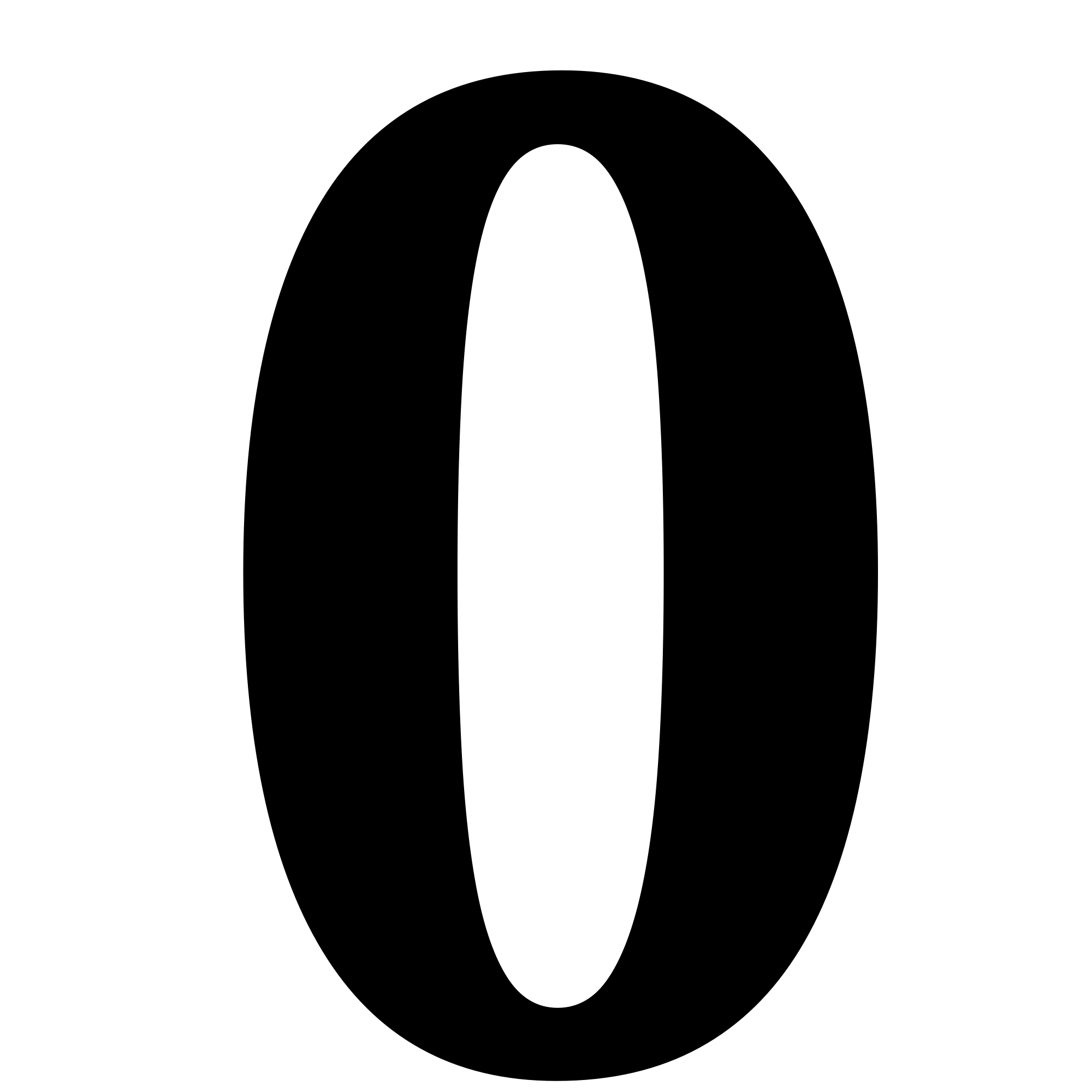0

Video: 0

    0 GudangMovies21 Rebahinxxi LK21

    0 dapat mengacu pada beberapa hal berikut:

    0 (angka), nol, bilangan bulat antara −1 dan +1
    Tahun 0, tahun (sama dengan 1 BC / SM) yang mendahului tahun 1 M dalam perhitungan astronomi

Kata Kunci Pencarian: 0

00001nonton010895 kartu apa07 2d togel0.99 dollar berapa rupiah00 2d togel0858 kartu apa04 2d togel Search Results

0

Daftar Isi

Is $0$ a natural number? - Mathematics Stack Exchange

Mar 15, 2013 · Inclusion of $0$ in the natural numbers is a definition for them that first occurred in the 19th century. The Peano Axioms for natural numbers take $0$ to be one though, so if you are working with these axioms (and a lot of natural number theory does) then you take $0$ to be a natural number.

factorial - Why does 0! = 1? - Mathematics Stack Exchange

$\begingroup$ The theorem that $\binom{n}{k} = \frac{n!}{k!(n-k)!}$ already assumes $0!$ is defined to be $1$. Otherwise this would be restricted to $0 <k < n$. A reason that we do define $0!$ to be $1$ is so that we can cover those edge cases with the same formula, instead of having to treat them separately.

Why does 0.00 have zero significant figures and why throw out …

Aug 10, 2023 · The measurement 0.00010 has 2 sigfigs (or in SN, 1.0e-4). A measurement with the same apparatus that reports 0.00000 should seemingly also have at least 2, but we cant determine that from the string. When ambiguous perhaps it must be written as 0.0e-4 or 0.00e-3 depending on the edge case convention?

algebra precalculus - Zero to the zero power – is $0^0=1 ...

Whereas exponentiation by a real or complex number is a messier concept, inspired by limits and continuity. So $0^0$ with a real 0 in the exponent is indeteriminate, because you get different results by taking the limit in different ways.

What is the integral of 0? - Mathematics Stack Exchange

Feb 4, 2018 · How about drawing sum upper and lower sums! You won't get very far because you'll be married to the horizontal axis and then, of course, all of the sums are zero and since a definite integral is always sandwiched between any upper and any lower sum. The value is trapped by 0. I.E. 0 <= the integral <= 0.

definition - Why is $x^0 = 1$ except when $x = 0$? - Mathematics …

Jan 22, 2017 · 1) x^a × x^b = x^a+b; for x = 0 and a = 0, you would get 0^0 × 0^b = 0^b = 0, so we can't tell anything -- except confirm that 0^0 = 1 still works here! 2) x^{-a}=1/{x^a} -- so when a = 0 , x^{-0} = 1/x^0 = x^0 , which again does work for 0^0 = 1 ; 3) {x^a}^b = x^{a×b} , thus x^(1/n) is the n-th root -- and 1/n = 0 for no value of n , so ...

I have learned that 1/0 is infinity, why isn't it minus infinity?

1 x 0 = 0. Applying the above logic, 0 / 0 = 1. However, 2 x 0 = 0, so 0 / 0 must also be 2. In fact, it looks as though 0 / 0 could be any number! This obviously makes no sense - we say that 0 / 0 is "undefined" because there isn't really an answer. Likewise, 1 / 0 is not really infinity. Infinity isn't actually a number, it's more of a concept.

What is $\\gcd(0,a)$, where $a$ is a positive integer?

Feb 24, 2019 · Thus it makes no sense to define $\rm\ gcd(0,8)\ $ to be $\,0\,$ or $\,1\,$ since $\,0\,$ is not a common divisor of $\,0,8\,$ and $\,1\,$ is not the greatest common divisor. The $\iff$ gcd definition is universal - it may be employed in any domain or cancellative monoid, with the convention that the gcd is defined only up to a unit factor.

What do zero eigenvalues mean? - Mathematics Stack Exchange

Dec 4, 2014 · If 0 is an eigenvalue, then the nullspace is non-trivial and the matrix is not invertible. Therefore all the equivalent statements given by the invertible matrix theorem that apply to only invertible matrices are false.

trigonometry - Why $\sin(n\pi) = 0$ and $\cos(n\pi)=(-1)^n ...

$\cdots \sin(-\pi), \sin(0), \sin(\pi), \sin(2\pi), \sin(3\pi),\cdots$ Which is exactly where the sine function has its roots, so it is always equal to $0$. For the cosine case, use the identity $\cos(x) = \cos(x + 2\pi) $ (period of the cosine function is $2\pi$) and plug $\cos(0)$ and $\cos(\pi)$ to …